Semestrální práce "Výměna na šachovnici"

 

Záhlaví

Jméno studenta:	David Šafránek, Martin Fiala
Studijní skupina:	5/38
Semestr, školní rok:	zimní 2005/2006
Katedra:	počítačů (K 13136)
Předmět:	Paralelní systémy a algoritmy (36PAR)
Seminář:	středa 16:15
Cvičící:	RNDr. Martin Nehéz
Přednášející:	Prof. Ing. Pavel Tvrdík, CSc.
Datum:	17.12.2005

 

Obsah

1. Definice problému a popis sekvenčního algoritmu
2. Popis paralelního algoritmu a jeho implementace v MPI
3. Naměřené výsledky a vyhodnocení
4. Literatura

Definice problému a popis sekvenčního algoritmu

Uloha VYM: vymena na sachovnici

Vstupni data:

m,n = prirozena cisla predstavujici velikost sachovnice S[1..m,1..n], m≥ n≥ 5
k = cele sude cislo predstavujici pocet cernych a bilych jezdcu, 1 ≤ k ≤ m*n-m

Definice:

Predpokladejme nasledujici cislovani policek sachovnice.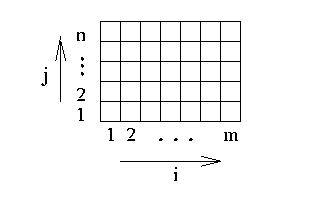

Sachovnice S[1..m,1..n].

Pak hlavni diagonala D je definovana nasledovne:

• Je-li m=n (sachovnice je ctvercova), pak hlavni diagonala D je mnozina policek S[i,i], i=1..m.
• Je-li m>n (sachovnice je obdelnikova) a
  • n deli m beze zbytku, pak hlavni diagonala je mnozina policek S[i,j], j=1,...,n a (j-1)*q < i ≤ j * q, kde q=m/n.
  • n nedeli m beze zbytku, pak hlavni diagonala se sklada ze skupin q policek, kde q=dolni_cela_cast(m/n). Jeji prvni polovina je mnozina policek S[i,j], j=1,...,dolni_cela_cast(n/2) a (j-1)*q < i ≤ j*q. Druha polovina diagonaly je symetricka podle stredove soumernosti. Pripadna zbyla policka jsou rovnomerne pridana k obema polovinam diagonaly (viz. obrazky).

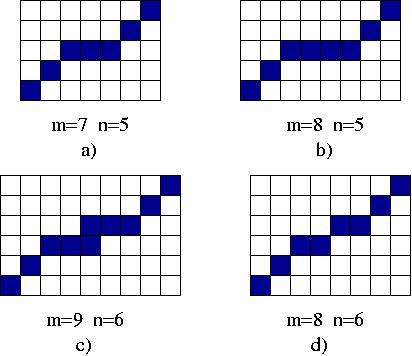
Priklady hlavnich diagonal D kdyz n nedeli m beze zbytku:
a) m a n jsou licha, b) m je sude a n je liche,
c) m je liche a n je sude, d) m a n jsou suda.

Mnozina jezdcu U obsahuje k/2 jezdcu umistenych po radcich v horni casti sachovnice S nad hlavni diagoalou D.

Mnozina jezdcu L obsahuje k/2 jezdcu umistenych po radcich v dolni casti sachovnice S pod hlavni diagoalou D.

Mnoziny U a L jsou stredove symetricke (viz dalsi obrazek).

Pravidla a cil hry:

Pocatecni stav je dan mnozinami U cernych jezdcu a L bilych jezdcu. Kazdy jezdec se muze na sachovnici pohybovat podle sachovych pravidel (tah ve tvaru pismene L a muze tahnout pouze na volne pole). Cilem hry je stridanim tahu bilych a cernych jezdcu prevest pocatecni stav na cilovy, ve kterem cerni jezdci obsadi oblast L a bili obsadi oblast U.

Ukol:

Nalezt minimalni posloupnost tahu bilych a cernych jezdcu vedouci z pocatecniho stavu do ciloveho.

Vystup algoritmu:

Cislo udavajici minimalni pocet tahu a vypis posloupnosti tahu vedoucich z pocatecniho do ciloveho stavu. Tahy zapisujte ve formatu dvojice pozic jezdce (odkud a kam jezdec v danem tahu tahnul).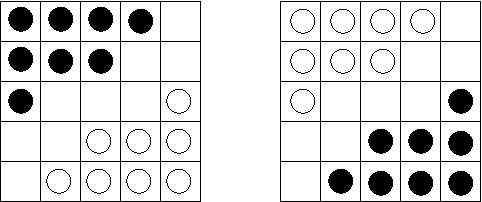

Pocatecni a cilovy stav pro n=m=5 a k=16.

Sekvencni algoritmus:

Sekvencni algoritmus je typu BB-DFS s neomezenou hloubkou (pri tazich jezdcu mohou vznikat cykly). Hloubku prohledavani musime omezit horni mezi (viz dale). Cena, kterou minimalizujeme, je pocet tahu. Protoze neni znama presna dolni mez na cenu reseni, algoritmus konci, kdyz prohleda cely stavovy prostor do hloubky dane horni mezi.

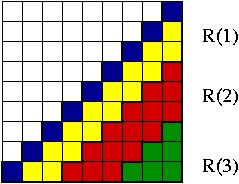
Pasy R(1),..,R(3) pro sachovnici m=n=9, ktere deli jezdce od prekroceni diagonaly.

Trivialni (nepresnou) dolni mez na pocet tahu lze odhadnout takto: Jezdci vzdy musi prekrocit diagonalu pri prechodu z mnoziny U do mnoziny L (ci naopak z L do U). Jestlize pro kazdeho jezdce na poli S[i,j] urcime minimimalni pocet tahu nutnych pro prekroceni diagonaly, tak soucet techto poctu pro vsechny jezdce je trivialni dolni mez. Sachovnici muzeme rozdelit do pasu R(k) podle tohoto poctu tahu k. Pas je siroky vzdy 3 policka sachovnice a kopiruje tvar diagonaly (viz. obrazek). Jestlize secteme soucty jezdcu v pasech R(k) a pocty tahu k, dostaneme nasledujici priblizny vyraz (plati pro m=n):

    n/3
2 * SUMA { j * sqrt [ (n-3(j-1))^2 + (n-3(j-1))^2  ] - 3 }
    j=1

Protoze se obecne jedna o znacne slozity vyraz, k vycisleni trivialni dolni meze pouzijte nasledujici program.

Presna horni mez na cenu reseni take neni znama. Vzhledem k moznym cyklum vsak potrebujeme aspon jeji odhad, aby bylo mozne orezavat stavovy prostor. Protoze kazdy jezdec dokaze projit celou sachovnici v mn tazich a tudiz v mnk tazich vsichni jezdci navstivi vsechna policka sachovnice, melo by byt reseni nalezeno maximalne v mnk tazich. Vzhledem k neexistenci presne dolni meze je nutne projit cely stavovy prostor do teto hloubky.

Poznámky k zadání

Algoritmus funguje pro instance velikosti 4x3x2 (mxnxk) až po zhruba 30x30x2. Maximální teoretická hodnota je dána velikostí buffery použitého pro reprezentace šachovnice s okraji. Zadaní je možné zjednodušit na pokládání jezdců jedné barvy zleva nahoře a duhé barvy zprava dole, protože díky složitosti nikdy nemůžeme položit více jezdců než je šířka řádku. Dále by se mohla zrušit podmínka m > n.

Inkrementální prohledávání

Protože neznáme přesně spodní a horní mez. Provádíme hledání s postupně se zvyšující (v našem případě o 2) prohledavanou hloubkou. Ve výsledku to na délku řešení nemá téměř žádný vliv i kdybychom přesnou hloubku znali, protože součet časů všech předchozích hloubek je jen zlomek trvání hloubky následující (exponencielní růst časů s vysokým základem).

Heuristiky

Ořezání stromu

Algoritmus je založen na podmínce, že zbývá-li k listu prohledávaného stromu méně úrovní než zbývajících jezdců, můžeme danou větev zanedbat.

Hash

Hash má velikost 16MB což činí při velikosti 8B na pozici 2M pozic. Jak je vidět z tabulek, pro instance trvající do 10ms způsobí hash zpomalení díky nutnosti vymazání při započetí výpočtu což trvá přibližně 8ms. Při větších instancích ale způsobí i exponenciální zrychlení, takže např. pro instanci 30x30x2 vrátí řešení za několik sekund, ale bez ní bychom se výsledku nedočkali nikdy. Vnaší úloze se význam hash projeví nejvíce při nižším počtu jezdců na šachovnici, kdy je stavový prostor nejmenší. Pro rozměry 10x10 (100 políček) a dvou jezdcích je stavový prostor velikosti 100*99=9900 možností.

Paralelni algoritmus:

Paralelni algoritmus je typu PBB-DFS-V, hledani darce algoritmem ACZ-AHD, deleni zasobniku pomoci D-ADZ.

Parametry programu

Podle zadání stačí pro určení zadání napsat par m n k.
Tedy např. pro šachovnici velikosti 10x5 se 2 jezdci na každé straně se zadá par 10 5 4.

Výstup algoritmu:

Solution found in depth 8.
d3-e1
b3-a5
c1-d3
c5-b3
b3-c1
d3-c5
a5-b3
e1-d3

Tahy jsou ve formátu zdrojové-cílové pole. Pole se značí písmenem udávajícím x-ovou souřadnici následovaným číslem udávajícím y-ovou souřadnici.

Tabulka naměřených časů pro různé instance:

Podrobná měření jsou v příloze.

Popis paralelního algoritmu a jeho implementace v MPI

Implementace

Pro přepis sekvenčního na paralelní řešení je potřeba mít naimplementované prohledávání stavového prostoru pomocí zásobníku, ale ne rekurzivním voláním funkcí.

Dynamické vyvažování zátěže

Má-li procesor prázdný zásobník žádá následující procesor o práci, dostane-li odpověď, že procesor práci nemá inkrementuje svůj lokální čítač a posílá znovu žádost.

Hledání dárce

Používáme metodu ACZ-AHD (asynchroni cyklicke zadosti): Kazdy procesor si udrzuje lokalni citac D, kde 1<= D <=p, oznacujici potencialniho darce.  Procesor s prazdnym zasobnikem posle zadost o praci procesoru P_D a inkrementuje citac D mod p. Muze se stat, ze jeden a tentyz procesor obdrzi nekolik zadosti o praci.

Dělení zásobníku

Používáme metodu D-ADZ (puleni u dna). Zadatel obdrzi zasobnik s jednou polovinou stavu co nejblize dnu.

Ukončení výpočtu

Probíhá pomocí algoritmu peška uvedeného v [1].

Granularita

Náš program má nastavenou granularitu počtem pozic které prozkoumá než se začne zabývat příchozími zprávami. Tento počet je nastaven na hodnotu 100 pozic, což odpovídá zhruba 100 000 lokálním operacím. Při vyšší hodnotě je granularita hrubá, odezva procesoru na zprávy příliš pomalá, a výpočtu se nezúčastní všechny procesory naráz. Při nižší hodnotě je granularita příliš jemná, a dochází k nadbytku režie.

Pro instance trvající do několika sekund (prozkoumává se málo pozic) se nevyplatí rozesílat ostatním procesorům data. V tomto případě se čas při zvýšení počtu procesorů nesníží, ale také nezvýší.

Naměřené výsledky a vyhodnocení

Pro měření paralelního času bylo nutné na začátek a na konec měření přidat bariéru, na které se všechny procesory sesynchronizují. Vzhledem k skokovým časům výpočtu, kdy zvýšení hloubky řešení o 2 znamená zvýšení času v stonásobcích. Proto bylo nalézt sekvenční instance trvající daný čas (5, 10, 15 minut) absolutně nemožné. Nelehké bylo i nalezení instance trvající podobný čas (2 minuty). Měření jsme provedli pro 2, 4, 8 a maximální možný počet dvanácti procesorů. Vzhledem k potřebné době stačilo pro 2 a 4 procesory vkládat do fronty bez parametru long.

Graf zrychlení a podrobná měření jsou v příloze.

K superlineárnímu zrychlení v naší úloze nedošlo. Důvod je, že sekvenční algoritmus uvažuje v prvním kroku ideální tah k řešení. Tudíž se řešení vyskytuje téměř na levém okraji prohledávaného stromu, a dělení u dna nezpůsobí, že by se řešení posunulo k jinému procesoru do levější části než původně. Měření potvrdilo, že sít mirinet je opravdu rychlejší než ethernetová. V našem případě zrychlení činilo přibližně 10%.

Pravděpodobně vhodnější místo dělení zásobníku u dna bylo použití dělení na prahu řežné výšky, režie by byla sice v tomto případě vyšší, ale pro nalezení prvního řešení by stačilo prozkoumat menší stavový prostor.

Závěr

Podařilo se nám porovnat sekvenční a paralelní algoritmus. Zrychlení paralelního algoritmu není ideální, ale existují i jiné typy úloh u kterých se dosahuje daleko lepších výsledků. Zvlášť když je k dispozici ještě více procesorů, než jsme měli k dispozici my. U takových rozsáhlých clusterů je třeba si dát pozor na rychlost režie, která může s počtem procesorů neadekvátně stoupat.

Literatura

1. Pavel Tvrdík: Paralelní systémy a algoritmy, Vydavatelství ČVUT, 1. vydání. Prosinec 2000
2. Hash tables

...