Úloha 3 z předmětu 36PAA
Zadání
Problém batohu
- Naprogramujte rešení 0/1 problému batohu metodou vetví a hranic tak, aby omezujícím faktorem byla hodnota optimalizacního kritéria.
- Naprogramujte rešení 0/1 problému batohu nebo alespoň 0/1 exaktního problému batohu bez cen metodou dynamického programování.
- Naprogramujte rešení 0/1 problému batohu heuristikou podle poměru cena/hmotnost s testem nejcennější věci.
| ID | počet kroku rešení | výsledná cena |
| ... | ... | ... |
Výsledky řešení problému batohu
Metoda
- Exaktní:
- Heuristika:
Závislost výpočetního času na n
Čas je uveden v instrukčních cyklech, kvůli odstíněnní závislosti na rychlosti procesoru. V řádu časové složitosti se to však neprojeví, jedná se pouze o multiplikativní konstantu.
Tabulka závislosti výpočetního času na n
Graf závislosti výpočetního času na n
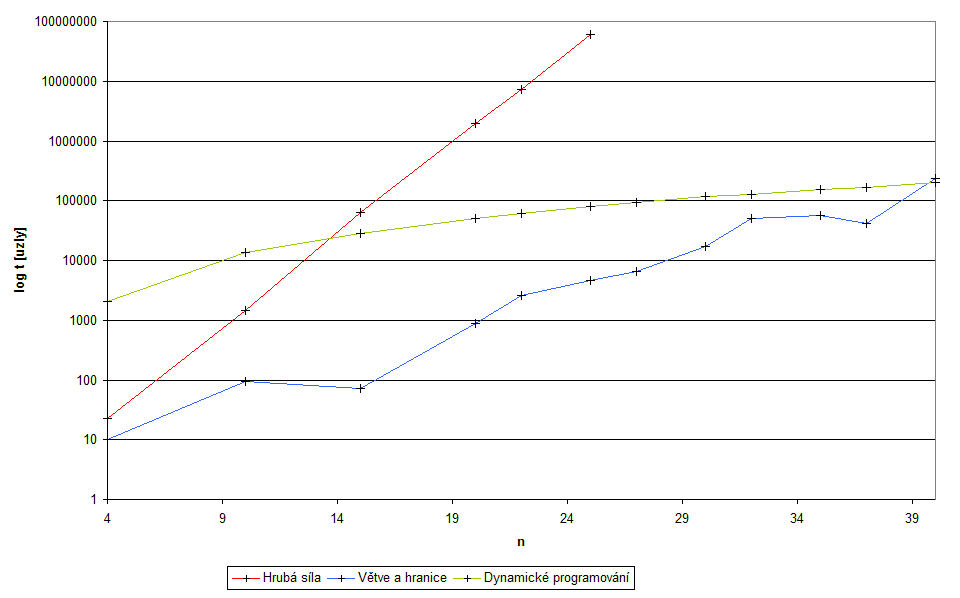
Jak je vidět, časová složitost metody dynamického programování je lepší zhruba pro n>40.
Tabulka porovnání dosažené ceny exaktní metody a heuristiky
Zdrojový kód
Závěr
Metoda větví byla použita již v první úloze - prohledávání se ukončí jakmile je překročeno omezující kritérium. Metoda hranic odkrojí ty větve, v kterých i při vložení všech následujících věcí nebude překročena nejlepší dosažená cena. Metoda větví a hranic sice ořeže značnou část stavového prostoru, avšak časová složitost zůstavé stále na úrovni hrubé síly. Metoda dynamického programování vrací stejné hodnoty jako metoda hrubé síly, je však asymptoticky odpovídající heuristice. Její jedinou nevýhodou je větší paměťová složitost. Rozdíl heuristik cena/váha a cena: průměrnou Relativní chybu má lepší 1. metoda (0,54% vs 1,68%), avšak max. relativní chybu metoda druhá (36,4% vs 24,8%). Heuristika nejnižší ceny se podle předpokladů ukázala jako nejhorší.
Pozn. Relativní chyba je dána |E-H| / E kde E je výsledek exaktní metody a H výsledek heuristiky.