Úloha 1 z předmětu 36PAA

Zadání

Základ problému

Je dáno

• celé číslo n (počet vecí)
• celé číslo M (kapacita batohu)
• konečná mnolina V={v₁, v₂, ..., v_n } (hmotnosti věcí)
• konečná mnolina C={c₁, c₂, ..., c_n } (ceny věcí)

0/1 problém batohu

Nejznámější varianta je optimalizacní. Pokud se mluví o "problému batohu" bez bližšího určení, vetšinou se rozumí tato verze.

Zkonstruujte množinu X={x₁, x₂, ... ,x_n }, kde každé x_i je 0 nebo 1, tak, aby

• platilo v₁x₁+v₂x₂ + ... + v_nx_n <= M
  (batoh nebyl pretížen).
• výraz c₁x₁+c₂x₂ + ... + c_nx_n
  nabýval maximální hodnoty pro vaechny takové množiny (cena vecí v batohu byla maximální).

Úloha

• Naprogramujte reaení 0/1 problému batohu hrubou silou. Na zkušebních datech pozorujte závislost výpočetního času na n.
• Naprogramujte rešení 0/1 problému batohu heuristikou podle poměru cena/váha. Pozorujte
  • závislost výpočetního času na n
  • průměrné zhoršení proti exaktní metodě
  • maximální chybu

Výsledkem bude krátká zpráva s naměřenými charakteristikami, doprovázená zdrojovými texty. Meření nechť je orientační - doba chodu jednotlivých testů nemusí překračovat několik málo minut. Rozsáhlejší experimenty jsou náplní pozdějších úloh.

Výsledky řešení problému batohu

Exaktní metoda

Heuristika

Závislost výpočetního času na n

Čas je uveden v instrukčních cyklech, kvůli odstíněnní závislosti na rychlosti procesoru. V řádu časové složitosti se to však neprojeví, jedná se pouze o multiplikativní konstantu.

Tabulka závislosti výpočetního času na n

Graf závislosti výpočetního času na n

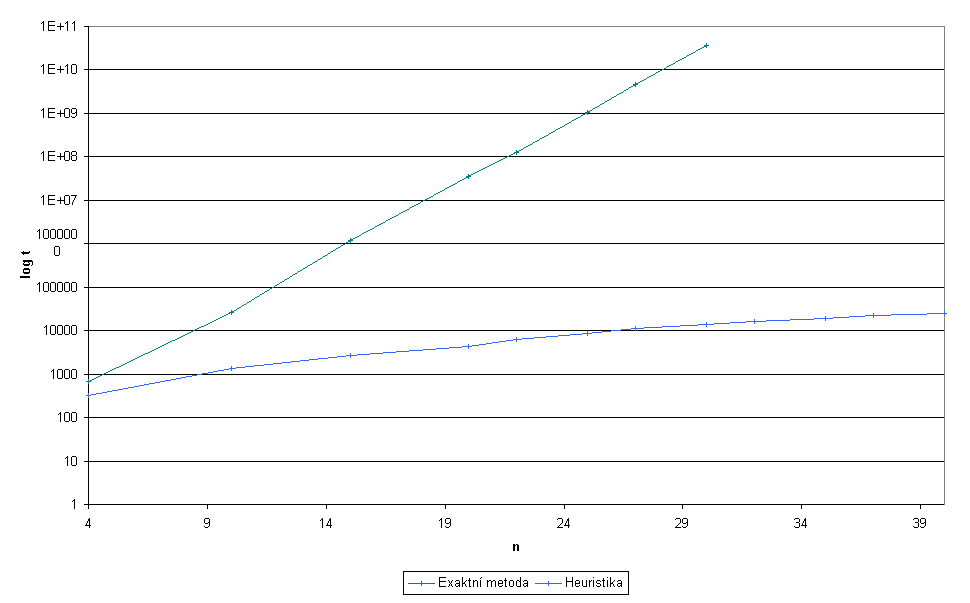
Jak je vidět, časová složitost exaktní metody stoupá exponencielně - O(2ⁿ), což je pro čísla řádu desítek už tak zdlouhavé, že se problém stává neřešitelným. Za použití heuristiky (poměr cena/váha) je časová složitost lineární - O(n) čož značí její dobrou kvalitu, dále ještě zjistíme jak mnoho se výsledky s použitím heuristiky liší od přesných.

Tabulka porovnání dosažené ceny exaktní metody a heuristiky

Průměrné zhoršení proti exaktní metodě

Absolutní hodnoty 9,7; relativně 0,54%.

Maximální chyba

Pro Id=9 080 dosáhla absolutní hodnoty 121; pro Id=9 037 dosáhla relativní chyba 36,4%.

Zdrojový kód

Závěr

Čas pro řešení hrubou silou jsem měřil jen pro n do 30. Při vyšších hodnotách už narůsta potřebný čas do řádů hodin. Průměrná hodnota heuristického řešení se příliš neliší, zato v rychlosti je rapidní rozdíl.